System dwójkowy
Powszechnie używany w elektronice cyfrowej, gdzie minimalizacja liczby stanów (do dwóch) pozwala na prostą implementację sprzętową odpowiadającą zazwyczaj stanom wyłączony i włączony oraz zminimalizowanie przekłamań danych[2]. System binarny przyjął się również w informatyce.
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciągi cyfr, z których każda jest mnożną kolejnej potęgi podstawy systemu.
Np. liczba zapisana w dziesiętnym systemie liczbowym jako 10, w systemie dwójkowym przybiera postać 1010, gdyż:
Dziesiętny system liczbowy
Dziesiętny system liczbowy, zwany też systemem decymalnym lub arabskim to pozycyjny system liczbowy, w którym podstawą pozycji są kolejne potęgi liczby 10. Do zapisu liczb potrzebne jest więc w nim 10 cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciąg cyfr, z których każda jest mnożnikiem kolejnej potęgi liczby stanowiącej podstawę systemu. Część całkowitą i ułamkową oddziela separator dziesiętny.
Np zapis "5045,7" wynika z: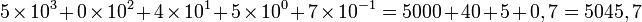
Pozycyjny, dziesiętny system liczbowy jest obecnie na świecie podstawowym systemem stosowanym niemal we wszystkich krajach. Oryginalnie pochodzi on z Indii, z których przedostał się do Europy za pośrednictwem Arabów. Od XVI wieku stosowano go obok systemu rzymskiego, w nauce, księgowości oraz tworzącej się właśnie bankowości, gdyż system ten znacznie upraszcza operacje arytmetyczne. W oficjalnych dokumentach jednak nadal zamieniano liczby w zapisie arabskim na system rzymski. W końcu, dzięki praktycznym zaletom system rzymski został prawie zupełnie wyparty na korzyść arabskiego.
System szesnastkowy
Do tej pory mówiliśmy o systemach, w których problemem było przedstawienie cyfr większych od podstawy systemu (jak zapisać dwójkę w systemie, który ma tylko dwie cyfry: 0 i 1?). W systemie szesnastkowym problem się odwraca - jak w jednym znaku zapisać liczbę o wartości dziesięć, czy piętnaście? Dlatego system szesnastkowy, inaczej heksadecymalny, używa oprócz dziesięciu cyfr także znaków: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Również ten system wykorzystywany jest jako sposób skracania liczb dwójkowych. Weźmy liczbę 11100010. Wystarczy pogrupować jej cyfry po cztery: 1110 0010 i zapisać każdą z tych czwórek za pomocą cyfr systemu heksadecymalnego. W tym wypadku będzie to 0E2h. Wyjaśnienia wymagają zero na początku i h na końcu zapisu. Przyjęło się stawiać zero na początku liczby szesnastkowej, o ile jej pierwszą cyfrą jest litera. Natomiast literka h na końcu oznacza, że liczba zapisana jest w systemie heksadecymalnym.
Jeśli chodzi o zastosowania systemu szesnastkowego, to należy wspomnieć o tym, że w tym systemie są kodowane adresy w pamięci operacyjnej, a także często liczby określające kolory.
